Sergey and me gave an interview on Shogun and Google Summer of Code. Here it is:
The internet. More specifically #shogun on irc.freenode.net. Wasn’t IRC that thing that our big brothers used as a socialising substitute when they were teenagers back in the 90s? Anyways. We are talking to two of the hottest upcoming figures in machine learning open-source software, the Russian software entrepreneur Sergey Lisitsyn, and the big German machine Heiko Strathmann.


Hi guys, glad to meet you. Would you mind introducing yourself?
Sergey (S): Hey, I am Sergey. If you ask me what do I do apart from Shogun – I am currently working as a software engineer and finishing my Master’s studies at Samara State Aerospace University. I joined Shogun in 2011 as a student and now I am doing my best to help guys from the Shogun team to keep up with GSoC 2014.
Heiko (H): Hej, my name is Heiko. I do a Phd in Neuroscience & Machine Learning at the Gatsby Institute in London and joined Shogun three years ago during GSoC. I love open-source since my days in school.
Your project, Shogun, is about Machine Learning. That sounds scary and sexy, but what is it really?
H: My grandmother recently sent me an email asking about this ‘maschinelles Lernen’. I replied it is the art of finding structure in data in an automated way. She replied: Since when are you an artist? And what is this “data”? I showed her the movie PI by Darren Aronofsky where the main character at some point is able to predict stock prices after realising “the pattern”, and said that’s what we want to do with a computer. Since then, she is worried about me because the guy puts a drill into his head in the end….. Another cool application is for example to model brain patterns to allow people to learn how to use a prosthesis faster.
S: Or have you seen your iPhone detects faces? That’s just a Support Vector Machine (SVM). It employs kernels which are inner products of non-linear mappings of Haar features into a reproducing kernel Hilbert Space so that it minimizes ….
Yeah, okok… What is the history of Shogun in the GSoC?
S: The project got started by Sören in his student days around 15 years ago. It was a research only tool for a couple of years before being made public. Over the years, more and more people joined, but the biggest boost came from GSoC…
H: We just got accepted into our 4th year in that program. We had 5+8+8 students so far who all successfully did the program with us. Wow I guess that’s a few million dollars. (EDITOR: actually 105,000$.) GSoC students forced Shogun to grow up in many ways: github, a farm of buildbots, proper unit-testing, a cloud-service, web-demos, etc were all set up by students. Also, the diversity of algorithms from latest research increased a lot. From the GSoC money, we were able to fund our first Shogun workshop in Berlin last summer.
How did you two got into Shogun and GSoC? Did the money play a role?
H: I was doing my undergraduate project back in 2010, which actually involved kernel SVMs, and used Shogun. I thought it would be a nice idea of putting my ideas into it — also I was lonely coding just on my own. 2010, they were rejected from GSoC, but I eventually implemented my ideas in 2011. The money to me was very useful as I was planning to move to London soon. Being totally broke in that city one year later, I actually paid my rent from my second participation’s stipend – which I got for implementing ideas from my Master’s project at uni. Since 2013, I mentor other students and help organising the project. I think I would have stayed around without the money, but it would have been a bit tougher.
S: We were having a really hard winter in Russia. While I was walking my bear and clearing the roof of the snow, I realised I forgot to turn off my nuclear missile system…..
H: Tales!
S: Okay, so on another cold night I noticed a message on GSoC somewhere and then I just glanced over the list of accepted organizations and Shogun’s description was quite interesting so I joined a chat and started talking to people – the whole thing was breathtaking for me. As for the money – well, I was a student and was about to start my first part-time job as a developer – it was like a present for me but it didn’t play the main role!
H: To make it short: Sergey suddenly appeared and rocked the house coding in lightspeed, drinking Vodka.
But now you are not paid anymore, while still spending a lot of time on the project. What motivates you to do this?
S: This just involves you and you feels like you participate in something useful. Such kind of appreciation is important!
H: Mentoring students is very rewarding indeed! Some of those guys are insanely motivated and talented. It is very nice to interact with the community with people from all over the world sharing the same interest. Trying to be a scientist, GSoC is also very useful in producing tools that myself or my colleagues need, but that nobody has the time to build properly. You see, there are all sorts of synergic effects in GSoC and my day-job at university, such as meeting new people or getting a job since you know how to code in a team.
How does this work? Did you ever publish papers based on GSoC work?
S: Yeah, I actually published a paper based on my GSoC 2011 work. It is called ‘Tapkee: An Efficient Dimension Reduction Library’ and was recently published in the Journal of Machine Learning Research. We started writing it up with my mentor Christian (Widmer) and later Fernando (Iglesias) joined our efforts. It took enormous amount of time but we did it! Tapkee by the way is a Russian word for slippers.
H: I worked on a project on statistical simulation of global ozone data last year. The code is mainly based on one of my last year’s student’s project – a very clever and productive guy from Mumbai who I would never have met without the program, see http://www.ucl.ac.uk/roulette/ozoneexample
So you came all the way from being a student with GSoC up to being an organisation admin. How does the perspective change during this path?
H: I first had too much time so I coded open-source, then too little money so I coded open-source, then too much work so I mentor people coding it open-source. At some point I realised I like this stuff so much that I would like to help organising Shogun and bring together the students and scientists involved. It is great to give back to the community which played a major role for me in my studies. It is also sometimes quite amusing to get those emails by students applying, being worried about the same unimportant things that I worried about back then.
S: It seems to be quite natural actually. You could even miss the point when things change and you became a mentor. Once you are into the game things are going pretty fast. Especially if you have full-time job and studies!
Are there any (forbidden) substances that you exploit to keep up with the workload?
S: It would sound strange but I am not addicted to vodka. Although I bet Heiko is addicted to beer and sausages.
H: Coffeecoffeecoffeee…… Well, to be honest GSoC definitely reduces your sleep no matter whether you are either student, mentor, or admin. By the way, our 3.0 release was labelled: Powered by Vodka, Mate, and beer.
Do you crazy Nerds actually ever go away from your computers?
H: No.
S: Once we all met at our workshop in Berlin – but we weren’t really away from our computers. Why on earth to do that?
Any tips for upcoming members of the open-source community? For students? Mentors? Admins?
H: Students: Do GSoC! You will learn a lot. Mentors: Do GSoC! You will get a lot. Admins/Mentors: Don’t do GSoC, it ruins your health. Rather collect stamps!
S: He is kidding. (whispers: “we need this … come on … just be nice to them”)
H: Okay to be honest: just have fun of what you are doing!
Due to the missing interest in the community, Sergey and Heiko interviewed themselves on their own.
Shogun: http://www.shogun-toolbox.org
GSoC 2013 blog: http://herrstrathmann.de/shogun-blog/110-shogun-3-0.html
GSoC 2014 ideas: http://www.shogun-toolbox.org/page/Events/gsoc2014_ideas
Heiko: http://herrstrathmann.de/
Sergey: http://cv.lisitsyn.me/






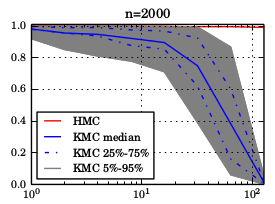


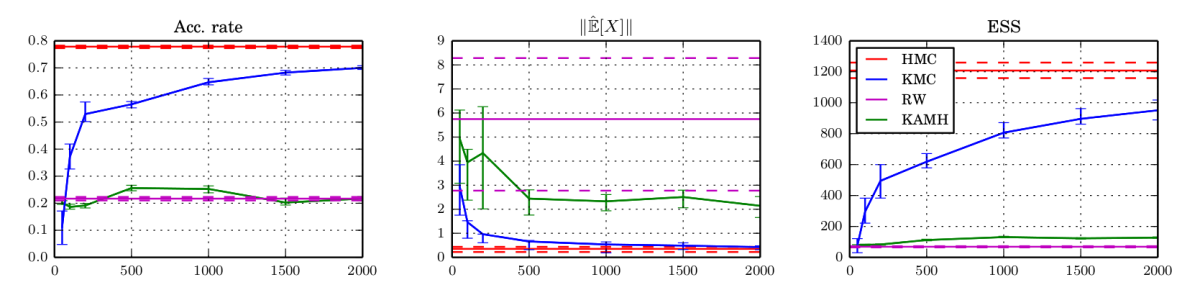
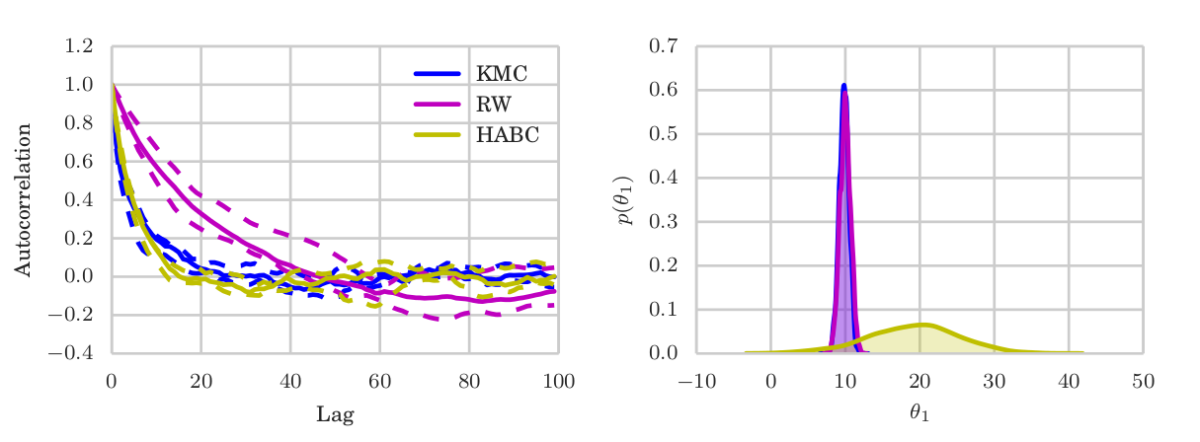

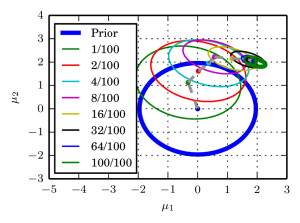

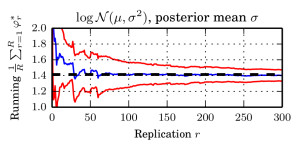


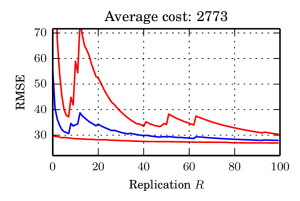
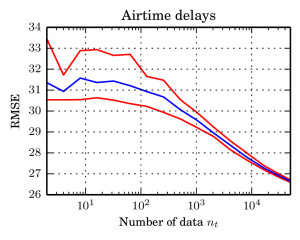





 We argue that there exists a class of posterior distributions for that HMC is not available, while the distribution itself is still highly non-linear. You get them as easy as attempting binary classification with a
We argue that there exists a class of posterior distributions for that HMC is not available, while the distribution itself is still highly non-linear. You get them as easy as attempting binary classification with a