NIPS 2012 is already over. Unfortunately, I could not go due to the lack of travel funding. However, as mentioned a few weeks ago, I participated in one paper which is closely related to my Master’s project with Arthur Gretton and Massi Pontil. Optimal kernel choice for large-scale two-sample tests. We recently set up a page for the paper where you can download my Matlab implementation of the paper’s methods. Feel free to play around with that. I am currently finishing implementing most methods into the SHOGUN toolbox. We also have a poster which was presented at NIPS. See below for all links.
Update: I have completed the kernel selection framework for SHOGUN, it will be included in the next release. See the base class interface here. See an example to use it: single kernel (link) and combined kernels (link). All methods that are mentioned in the paper are included. I also updated the shogun tutorial (link).
At its core, the paper describes a method for selecting the best kernel for two-sample testing with the linear time MMD. Given a kernel $k$ and terms
$$h_k((x_{i},y_{i}),((x_{j},y_{j}))=k(x_{i},x_{i})+k(y_{i},y_{i})-k(x_{i},y_{j})-k(x_{j},y_{i}),$$
the linear time MMD is their empirical mean,
$$\hat\eta_k=\frac{1}{m}\sum_{i=1}^{m}h((x_{2i-1},y_{2i-1}),(x_{2i},y_{2i})),$$
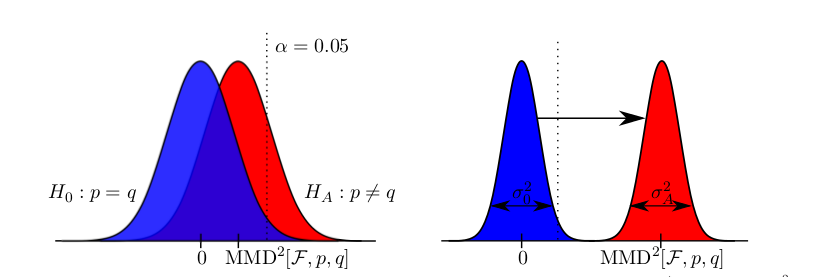
which is a linear time estimate for the squared distance of the mean embeddings of the distributions where the $x_i, y_i$ come from. The quantity allows to perform a two-sample test, i.e. to tell whether the underlying distributions are different.
Given a finite family of kernels $\mathcal{K}$, we select the optimal kernel via maximising the ratio of the MMD statistic by a linear time estimate of the standard deviation of the terms
$$k_*=\arg \sup_{k\in\mathcal{K}}\frac{ \hat\eta_k}{\hat \sigma_k},$$
where $\hat\sigma_k^2$ is a linear time estimate of the variance $\sigma_k^2=\mathbb{E}[h_k^2] – (\mathbb{E}[h_k])^2$ which can also be computed in linear time and constant space. We give a linear time and constant space empirical estimate of this ratio. We establish consistency of this empirical estimate as
$$ \left\vert \sup_{k\in\mathcal{K}}\hat\eta_k \hat\sigma_k^{-1} -\sup_{k\in\mathcal{K}}\eta_k\sigma_k^{-1}\right\vert=O_P(m^{-\frac{1}{3}}).$$
In addition, we describe a MKL style generalisation to selecting weights of convex combinations of a finite number of baseline kernels,
$$\mathcal{K}:={k : k=\sum_{u=1}^d\beta_uk_u,\sum_{u=1}^d\beta_u\leq D,\beta_u\geq 0, \forall u\in{1,…,d}},$$
via solving the quadratic program
$$\min_\beta { \beta^T\hat{Q}\beta : \beta^T \hat{\eta}=1, \beta\succeq 0},$$
where $\hat{Q}$ is the positive definite empirical covariance matrix of the $h$ terms of all pairs of kernels.
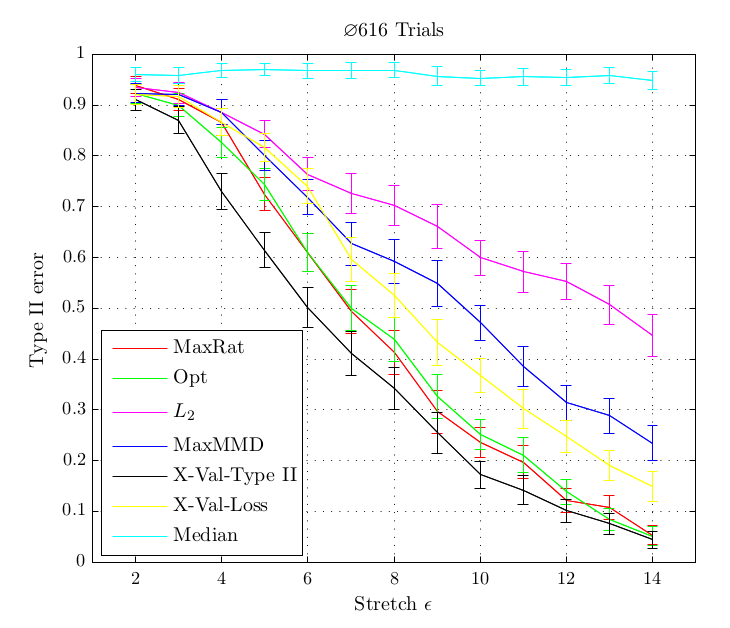
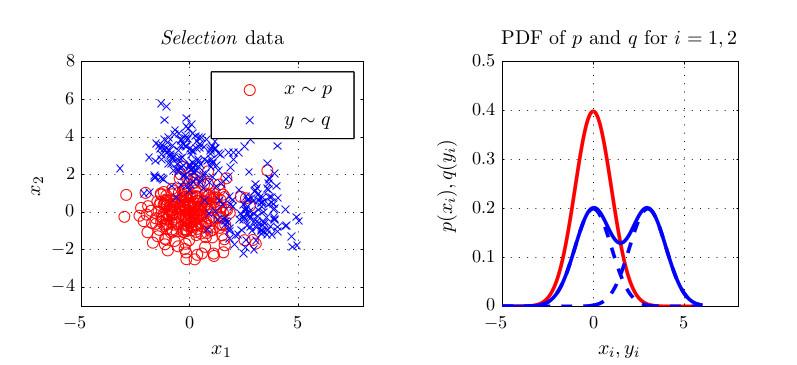
We then describe three experiments to illustrate
- That our criterion outperforms existing methods on synthetic and real-life datasets which correspond to hard two-sample problems
- Why multiple kernels can be an advantage in two-sample testing
See also the description of my Master’s project (link) for details on the experiments.
Download paper
Download poster
Download Matlab code (under the GPLv3)
Supplementary page

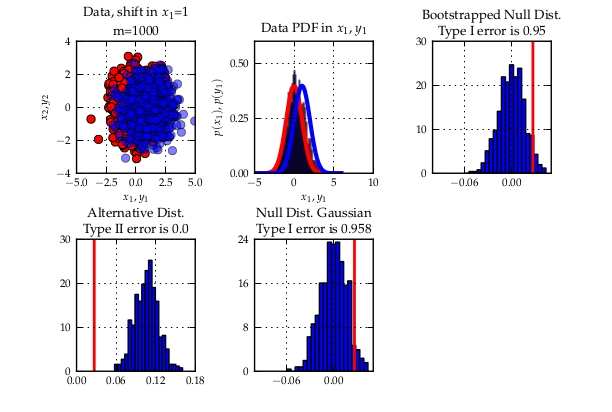
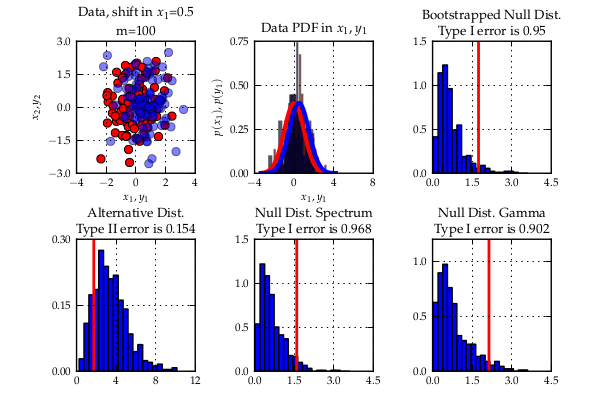
 a quadratic time test on the maximum processable amount of data reached a bad type II error while with the linear time version and much more data, almost zero type II error could be reached. Another case is when simply infinite data (but finite computation time) is available: the (adaptive) linear time test reaches lower type II error that its quadratic counterpart.
a quadratic time test on the maximum processable amount of data reached a bad type II error while with the linear time version and much more data, almost zero type II error could be reached. Another case is when simply infinite data (but finite computation time) is available: the (adaptive) linear time test reaches lower type II error that its quadratic counterpart.

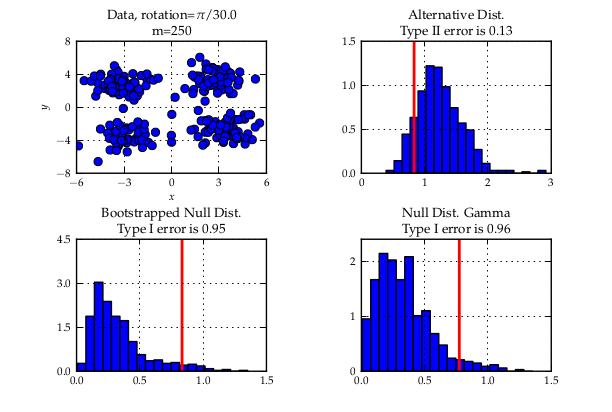
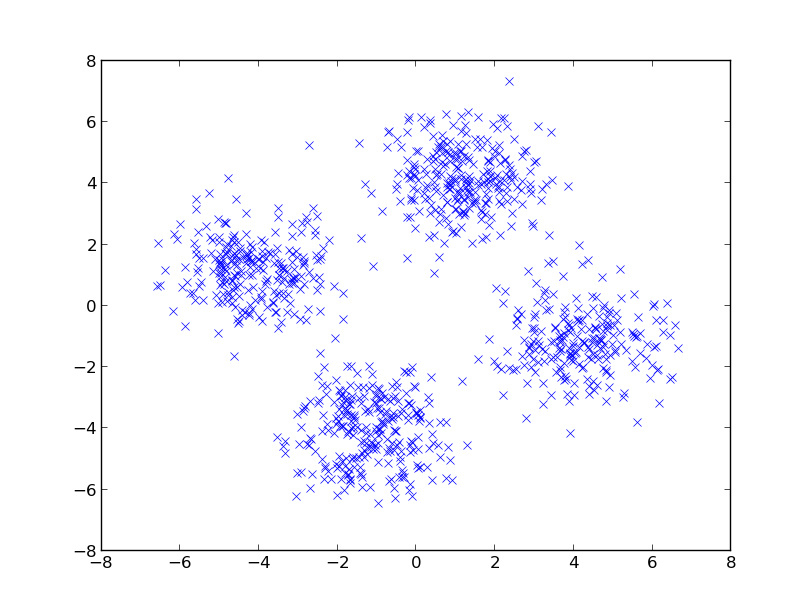
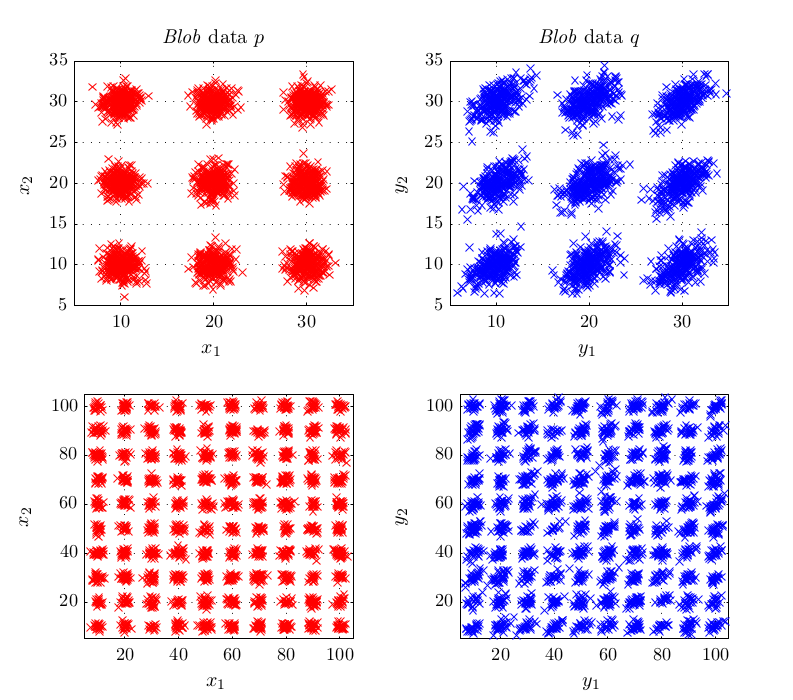
 In experiments, this criterion performed better or at least equal than existing methods for kernel selection. This is especially true when the length scale at which probability distributions differ is different to the overall length scale, as for example in the above shown blobs dataset.
In experiments, this criterion performed better or at least equal than existing methods for kernel selection. This is especially true when the length scale at which probability distributions differ is different to the overall length scale, as for example in the above shown blobs dataset.