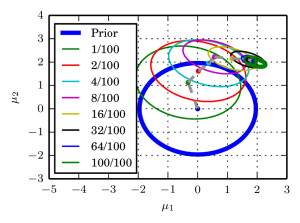
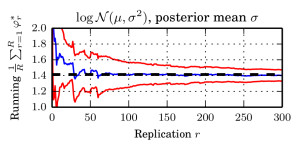
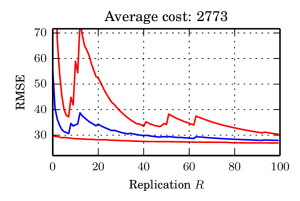
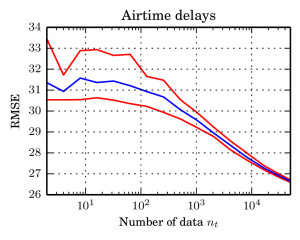
Updates:
December 2015: The journal version of the paper finally got published — after just three years.
While I was working at UCL’s Statistics Department in winter, I got involved into a very exciting project in the group of Mark Girolami. It is based around the Pseudo-Marginal Metropolis-Hastings algorithm. In 2003, a Genetics paper [1] described an approach to sample a distribution using the standard Metropolis-Hastings algorithm when the density function is not available by simply replacing it with an unbiased estimate.
For a standard Bayesian inference problem with likelihood $\pi(y|\theta) $, prior $\pi(\theta)$, and a proposal $Q$, rather than using the standard M-H ratio $$\frac{\pi(y|\theta^{\text{new}})}{pi(y|\theta)}\times\frac{\pi(\theta^{\text{new}})}{\pi(\theta)}\times \frac{Q(\theta|\theta^{\text{new}})}{Q(\theta^{\text{new}}|\theta)},$$ the likelihood is replaced by an unbiased estimator as
$$\frac{\hat{\pi}(y|\theta^{\text{new}})}{\hat{\pi}(y|\theta)}\times\frac{\pi(\theta^{\text{new}})}{\pi(\theta)}\times \frac{Q(\theta|\theta^{\text{new}})}{Q(\theta^{\text{new}}|\theta)}.$$ Remarkably the resulting Markov chain converges to the same posterior distribution as the exact algorithm. The approach was later formalised and popularised in [2].
In our project, we exploited this idea to perform inference over models whose likelihood functions are intractable. Example of such intractable likelihoods are for example Ising models or, even simpler, very large Gaussian models. Both of those models’ normalising constants are very hard to compute. We came up with a way of producing unbiased estimators for the likelihoods, which are based on writing likelihoods as an infinite sum, and then truncating it stochastically.
Producing unbiased estimators for the Pseudo-Marginal approach is a very challenging task. Estimates have to be strictly positive. This can be achieved via pulling out the sign of the estimates in the final Monte-Carlo integral estimate and add a correction term (which increases the variance of the estimator). This problem is studied under the term Sign problem. The next step is to write the likelihood function as an infinite sum. In our paper, we do this for a geometrically titled correction of a biased estimator obtained by an approximation such as importance sampling estates, upper bounds, or deterministic approximations, and for likelihoods based on the exponential function.
I in particular worked on the exponential function estimate. We took a very nice example from spatial statistics: a worldwide grid of ozone measurements from a satellite that consists of a about 173,405 measurements. We fitted a simple Gaussian model whose covariance matrices are massive (and sparse). In such models of the form $$ \log \mathcal{N}_x(\mu,\Sigma))=-\log(\det(\Sigma)) – (\mu-x)^T \Sigma^{-1}(\mu-x) + C, $$ the normalising constant involves a log-determinant of such a large matrix. This is impossible using classical methods such as Cholesky factorisation $$\Sigma=LL^T \Rightarrow \log(\det(\Sigma))=2\sum_i\log(L_{ii}),$$ due to memory shortcomings: It is not possible to store the Cholesky factor $L$ since it is not in general sparse. We therefore constructed an unbiased estimator using a very neat method based on graph colourings and Krylov methods from [3].

This unbiased estimator of the log-likelihood is then turned into a (positive) unbiased estimator of the likelihood itself via writing the exponential function as an infinite series $$\exp(\log(\det(\Sigma)))=1+\sum_{i=1}^\infty \frac{\log(\det(\Sigma))^i}{i!}. $$
We then construct an unbiased estimator of this series by playing Russian Roulette: We evaluate the terms in the series and plug in a different estimator for $\log(\det(\Sigma))$ for every $i$; once those values are small, we start flipping a coin every whether we continue the series or not. If we do continue, we add some weights that ensure unbiasedness. We also ensure that it is less likely to continue in every iteration so that the procedure eventually stops. This basic idea (borrowed from Physics papers from some 20 years ago) and some technical details and computational tricks then give an unbiased estimator of the likelihood of the log-determinant of our Gaussian model and can therefore be plugged into Pseudo-Marginal M-H. This allows to perform Bayesian inference over models of sizes where it has been impossible before.
More details can be found on our project page (link, see ozone link), and in our paper draft on arXiv (link). One of my this year’s Google summer of Code projects for the Shogun Machine-Learning toolbox is about producing a sophisticated implementation of log-determinant estimators (link). Pretty exciting!
[1]: Beaumont, M. A. (2003). Estimation of population growth or decline in genetically monitored populations. Genetics 164 1139–1160.
[2]: Andrieu, C., & Roberts, G. O. (2009). The pseudo-marginal approach for efficient Monte Carlo computations. The Annals of Statistics, 37(2), 697–725.
[3]: Aune, E., Simpson, D., & Eidsvik, J. (2012). Parameter Estimation in High Dimensional Gaussian Distributions.